2物体の運動

糸でつながれた2物体問：水平と30°の角をなす粗い斜面上に質量 m の物体Aをのせ、これに糸をつないで滑車をへて同じ質量の物体Bをつるす。手を放すとAは斜面に沿って滑り上がった。動摩擦係数を0.5、重力加速度の大きさをg とする。

１．糸の張力とA、Bの加速度の大きさを求めよ。
２．滑車が糸から受ける合力の大きさはいくらか。

**図 1:**糸でつながれた2物体

△上へ戻る

問い１

1.まずは図1がどのように動いているかを、加速度ベクトルを用いて図示してみましょう。

**図 2:** 物体の移動方向

では、この図2において、それぞれの物体A、Bに働く力を図示してみます。（滑車は気にしていません。あくまでもそれぞれの物体A、Bに働く力です。物体の運動方向は赤色の矢印で、運動方向と垂直な方向の力は緑色の矢印で表しています。）

**図 3:** 物体に作用する力を書き込む

図3において、A、Bそれぞれにおける運動方程式を、運動方向を正として（図3の加速度矢印の方向を正として）たてると、

$\displaystyle A:\quad ma$	$\displaystyle = T -mg\sin 30°- \frac{1}{2}mg\cos 30°$	(1)
$\displaystyle B:\quad ma$	$\displaystyle = mg - T$	(2)

となります。式(1)と式(2)より、

$\displaystyle a =$	$\displaystyle \frac{2 - \sqrt{3}}{8}g$	(3)
$\displaystyle T =$	$\displaystyle \frac{6 + \sqrt{3}}{8}mg$	(4)

と求められます。は設問に求められてはいませんが、次の問題で使うのでここで求めておきました。

△上へ戻る

問い2

2.では次に滑車にかかる力ですが、まずは図2において全体図内で滑車にどのように力が働いているかを図示してみます。

**図 4:** 滑車に働く力の大きさと方向

このようになっていますね。このは当然物体Aや物体Bに働いていた糸からの張力と同じ大きさのものです。では滑車だけに注目して、大きく図示しなおしてみましょう。

**図 5:** 滑車に注目

設問で求められているのは、この滑車の2点に働いている力を一つにまとめた合力なわけです。では、剛体（硬くて力を加えても曲がらない物体）に働く力の合成を考えます。図5の滑車は剛体なので、それぞれの力のベクトルの支点を合わせて

**図 6:** ベクトルの支点を合わせる

この2ベクトルを合成した合成ベクトルは図7の青いベクトルとなります。

**図 7:**ベクトルの合成

ではこの合成ベクトルの大きさを求めてみましょう。もちろん色んな方法はありますが、ベクトルとして解くのならば、30°傾いたベクトルを水平方向のベクトルと鉛直方向のベクトルに分割したり、または、角度を利用して一気にまとめて解く方法もあります。さらには余弦定理を用いても解けますね。

＜ベクトルの分割その１＞

**図 8:** ベクトルの分割・合成

上にあった30°傾いたベクトルを、鉛直向きのベクトルの先に付け、そこから水平方向と鉛直方向へ分解したものが図8になります。そうすると、合成ベクトルの鉛直成分と水平成分は図より

$\displaystyle 鉛直成分： Tv =$	$\displaystyle T + T\sin 30°= \frac{3}{2}T$	(5)
$\displaystyle 水平成分： Th =$	$\displaystyle T\cos 30°= \frac{\sqrt{3}}{2}T$	(6)

となります。つまり

**図 9:** まとめ

図9から、直角三角形の斜辺の長さを求めればよいので、三平方の定理より

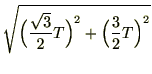$\displaystyle T' =$	$\displaystyle \sqrt{\Bigl(\frac{\sqrt{3}}{2}T\Bigr)^2 + \Bigl(\frac{3}{2}T\Bigr)^2}$
$\displaystyle =$	$\displaystyle \sqrt{3}\ T$	(7)

したがって、がであることがわかります。

＜ベクトルの分割その2＞
平行四辺形の各辺が同じ大きさだということに注目すると、

**図 10:** 対称性に注目

そうすると、ベクトル方向とそれに垂直な方向へ各ベクトルを分解して、

**図 11:** ベクトルの分解

緑色の分解されたベクトル $T\sin 30°$ はともに打ち消しあうので、赤色のベクトル $T\cos 30°$ のみが残り、それが各ベクトルから合計で2つ生じるので、その合力がとなります。

$\displaystyle T' =$	$\displaystyle 2T\cos 30°$
	$\displaystyle = 2\cdot \frac{\sqrt{3}}{2}T$
	$\displaystyle = \sqrt{3}\ T$	(8)

＜余弦定理の利用＞
最後に余弦定理を利用する方法を考えてみましょう。

**図 12:** Tベクトル同士のなす角に注目する

図12に示すようにベクトル同士のなす角は120°で、濃くなっている三角形で余弦定理より

$\displaystyle T' =$	$\displaystyle \sqrt{ T^2 + T^2 - 2\cdot T\cdot T\cos 120°}$
$\displaystyle =$	$\displaystyle T\sqrt{1 + 1 - 2\cdot 1 \cdot 1 \cdot\Bigl(-\frac{1}{\ 2\ }\Bigr)}$
	$\displaystyle = \sqrt{3}\ T$	(9)

このように、合成ベクトルの求め方は素直にベクトルを合成して考えるほかに、図形としての認識から問題を解く方法などがあります。ベクトルの合成が苦手なら、まず数の「ベクトルの合成」から見直すことをお勧めします。合成程度なら、最初の数ページの内容で十分ですから。

剛体の扱いがわからない場合は、力学の分野の「剛体」の部分を復習してください。モーメントの分野にも影響してきます。

△上へ戻る

トップページへ | 目次へ

ホーム＞ばねの問題