関数とは

x=βについて対称移動

ここまで来ると、この「 $x=\beta$ に関して対称移動」や次の「 $(x,y)=(\alpha,\beta)$ に関して対称移動」なんかももう見当がついていることだと思います。それほど説明も必要ないと思いますので、考え方とその結果だけを示しますね。一番下でちょっとした式変形時のコツをお教えします。これがわかると実はもっと簡単に式が作成できます。

$x=\beta$ に関して対称移動の場合、対称軸である $x=\beta$ と似た軸は軸です。そこで我々が知っているのは平行移動と、軸、軸対称移動だけですから、「 $y=\alpha$ に関する対称移動」y=αで対称移動へ飛びますか？のときと同様に、まずは対称軸 $x=\beta$ をy軸に重ねます。そして軸に関して対称移動したあとで、また対称軸ごと関数をもとの位置へ平行移動して戻します。これで終了です。作業をまとめると

対称軸をy軸に重ねる（関数もともに移動）
y軸対称移動
対称軸と関数とともに元の位置へ戻す

△上へ戻る

一般的な関数で

まずは一般的な関数y=f(x)でその様子を見てみましょうか。

**図 78:** 一般的なy=f(x)と対称軸x=β

このと対称軸 $x=\beta$ をともに軸の負方向へ $\beta$ だけ平行移動します。

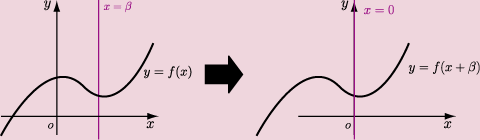**図 79:** x軸負方向へβ平行移動式(76)へ戻る

関数を軸に関して対称移動してみます。

**図 80:** y軸に関して対称移動式(77)へ戻る

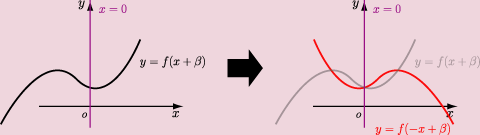最後に対称軸と関数をもとに戻したら終わりです。軸方向へ $\beta$ だけ平行移動しましょう。

**図 81:** y軸に関して対称移動

ではこれらを式にしてみましょう。

$\displaystyle y$	$\displaystyle = f(x+\beta)$	(76)式(76)：図79へ
$\displaystyle y$	$\displaystyle = f(-x + \beta)$	(77)式(77)：図80へ
$\displaystyle y$	$\displaystyle = f\{-(x -\beta)+\beta\}$	(78)式(78)：図81へ
$\displaystyle y$	$\displaystyle =f(-x+2\beta)$	(79)

グラフ中にも同様の式を入れていますので、それぞれ確認してみてください。

△上へ戻る

具体例にて

という具体的な関数をについて対称移動したグラフの図と式を考えて、どんな関数にも適用できるという確認をしておきます。

**図 82:** y=x²-2x+1のグラフと対称軸x=2

この図82で表されたグラフを図83のようにに関して対称移動します。

**図 83:** x=2に関して対称移動下へ戻る

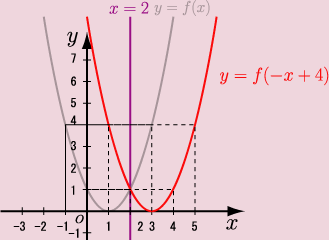出来上がったグラフの式は図83中でも示していますが、以下のような過程を経て

$\displaystyle y$	$\displaystyle = f(x+2)$
$\displaystyle y$	$\displaystyle = f(-x + 2)$
$\displaystyle y$	$\displaystyle = f\{-(x -2)+2\}$
$\displaystyle y$	$\displaystyle =f(-x+4)$	(80)

式(80)のようにと表されます。この値をに当てはめてみますと

$\displaystyle y$	$\displaystyle =f(-x+4)$
	$\displaystyle =(-x+4)^2-2(-x+4)+1$
	$\displaystyle =x^2 -8x + 16 +2x -8 +1$
	$\displaystyle =x^2 -6x +9$	(81)
	$\displaystyle =(x-3)^2$	(82)

となります。式(81)がの降べきの順に並べた式で、それを平方完成したのが式(82)になります。この式(82)と図83図83を確認を見比べるとを正しくに関して対称移動した後のグラフを表していることが分かりますね。

つまり、

x=β に関して対称移動と言われたら、対称軸をy軸にあわせ、そこで関数をy軸に関して対称移動し、対称軸と関数を元の位置に戻したら終了！

ということです。

△上へ戻る

おまけ

最後にテクニックなんですが…もう一度一般的な関数を $x=\beta$ に関して対称移動する場合の式変形をみてください。

$\displaystyle y$	$\displaystyle = f(x+\beta)$	(83)
$\displaystyle y$	$\displaystyle = f(-x + \beta)$	(84)
$\displaystyle y$	$\displaystyle = f\{-(x -\beta)+\beta\}$	(85)
$\displaystyle y$	$\displaystyle =f(-x+2\beta)$	(86)

ここで式(83)は絶対になくならない！ということと、その平行移動する方の変数（今回は）にその後「－」が付くということさえ覚えておけば、 $\beta$ は必ず2倍されますから、一般的な関数を $x=\beta$ に関して対称移動する場合

$\displaystyle y$	$\displaystyle =f(x)$
$\displaystyle y$	$\displaystyle = f(x+\beta)$	(87)
	$\displaystyle y=f(-x + 2\beta)$	(88)

と2つの式変形で求めることができます。私の場合は式(87)を一度わざと書いて、何が（今回は）どういう値（今回は $\beta$ ）で平行移動するのかを確かめてから一気に変形するようにしています。

△上へ戻る

トップページへ | 数学トップページへ | アーカイブス | 次へ：点対称 | 戻る：対称移動

考え方 | 一般的な関数で | 具体例で | おまけ

ホーム＞数学のトップページ＞関数の目次＞関数とは＞対称移動＞ x=βで対称移動

関数とは

x=βについて対称移動

x=βで対称移動の考え方

一般的な関数で

具体例にて

おまけ