力学

バネの直列接続

まずは直列接続と並列接続のイメージからお話しましょう。私の観点からいくと


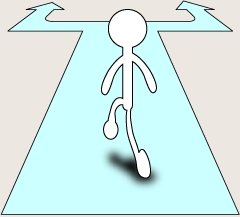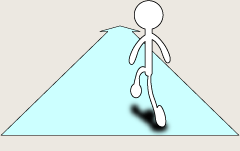
図20：直列のイメージ	図21：並列のイメージ

直列とは図20のように、回路（道）に沿って進んでいくと、ずっとまっすぐに進めるタイプの接続で、並列とは図21のように途中で二股に分かれていてどちらに行くか悩むタイプの接続になります。このイメージの利用に関してましては、また電気の回路に関する説明をするときにご説明いたします。（いつになることやら…）

△上へ戻る

バネの直列接続と合成

バネ定数が[N/m]のバネ1と[N/m]のバネ2とを直列接続してみます。そうすると図22のようになりますね。

**図 22:** 2本のバネを直列接続

これを

**図 23:** 2本のバネを合成したと考える

のように一つのバネとして考えてみたいわけです。これを教科書等では公式として、合成バネ定数[N/m]は

$\displaystyle \frac{1}{K}=\frac{1}{k_1}+ \frac{1}{k_2}$

(7)

と表しますよねまぁ私としてはこの式(7)の表記法は嫌いなのですが…嫌いな理由は下で…。しかしこれでは何が何やらわからないわけです。どうして？という疑問を持ちながら、「しかしまぁそう覚えろってことね」という妥協点を見つけて覚えている方がほとんどでしょう。ですが、そこで考えてみましょう。どうしてこういう公式になるんだろうと…。

△上へ戻る

公式の導出

まずはその2つが直列接続されたバネを先ほどと同様、少女に力[N]で引いてもらいましょう。

**図 24:** 2本のバネを直列にして引く

この状態でバネ1とバネ2にはどのような力が働いているかわかりますか？もちろん

**図 25:** バネ1、バネ2に働く力

のようになりますね。力の矢印が重なりますので、青のバネが発揮する力は上部に移動して示してあります。それぞれのバネには1巻きで考えたときと同じようにそれぞれの両端に、バネを伸ばす方向へ[N]の力が発生します。ということはバネ1、バネ2のバネ中のそれぞれ1巻きにおいても同様に力[N]が両端にかかりますね。

**図 26:** 1巻きのバネにかかる力

ですから、結局バネ1やバネ2が単独で[N]をかけられたのと同じだけ伸びるわけです。

**図 27:** それぞれのバネの伸び

これを式にしてみましょう。

$\displaystyle x_1$	$\displaystyle = \frac{F}{k_1}$	(8)
$\displaystyle x_2$	$\displaystyle = \frac{F}{k_2}$	(9)

となります。つまりバネ1とバネ2の伸びを合わせたトータルの伸び $x_{total}$ は

$\displaystyle x_{total}$	$\displaystyle = x_1 + x_2$
	$\displaystyle = \frac{F}{k_1} + \frac{F}{k_2}$
	$\displaystyle = \left( \frac{1}{k_1} + \frac{1}{k_2} \right)F$	(10)

ですね。ここでバネ1、バネ2をもともと1本のバネだったと考えて1本に図23のように合成するんでした。

**図 27(b):** 直列バネの合成

このときバネの伸び $x_{total}$ は合成バネのバネ定数を[N/m]として

$\displaystyle x_{total} = \frac{F}{K}$

(11)

と表されます。この式(11)は式(10)と同値ですので、つまり

$\displaystyle \frac{F}{K}$	$\displaystyle = \left( \frac{1}{k_1} + \frac{1}{k_2} \right)F$
$\displaystyle \frac{1}{K}$	$\displaystyle = \frac{1}{k_1} + \frac{1}{k_2}$	(12)

となりました。これでバネを直列接続したときは合成バネ定数[N/m]が式(12)のように表されることは納得してもらえたと思います。

△上へ戻る

式のイメージ

しかしこれで終わりではないのです。私は式(12)の形があまり好きではないのです。なぜなら、確かにきれいな形はしていますが、意味が取り辛いからです。意味が取り辛い式というのはつまりイメージがしにくい・わからない式ということで、したがって丸暗記を強要するという悲しい結果をもたらします。ですから式(12)を、意味が取り易い形に変形してみましょう！

式(12)を式変形してみます。

$\displaystyle K = \frac{k_1k_2}{k_1 + k_2}$

(13)

もちろんこの式変形は大丈夫ですよね。ではこの意味を考えてみましょう。この式(13)は

$\displaystyle K$	$\displaystyle = \frac{k_1}{k_1 + k_2}\cdot k_2$	(14)
	$\displaystyle =\frac{k_2}{k_1 + k_2}\cdot k_1$	(15)

のように変形できます。この式(14)、(15)において $\frac{k_1}{k_1 + k_2}$ や $\frac{k_2}{k_1 + k_2}$ はどのような値でしょうか？…そう必ず1より小さい値となります。だって $\frac{k_1}{k_1 + k_2}$ において、もし $\frac{k_1}{k_1}$ なら1ですが分母に正の値であるが1つ入ってとなると必ず分子のよりも大きくなりますから、 $\frac{\mbox{小さいもの}}{\mbox{大きいもの}}$ だったら絶対に1よりも小さくなりますよね。

**図 28:** 式の意味

ということは式(14)や式(15)は何を言っているかといいますと、はとのうち、小さい方よりも小さいということを言っているわけです。分かりますか？式(14)ではk₂よりも小さく、式(15)ではk₁よりも小さいと言っていますので、そのどちらか小さい方よりも小さくなるわけです。

つまりバネを直列に接続することによりバネ定数が小さい方よりもさらに小さくなってしまうわけです。しかしこれは何故でしょう？

△上へ戻る

より深く理解する

これは先ほどから図入りで説明している内容をきちんと理解している方であれば、すぐにわかります。まずはバネの伸びが[m]であったときにバネが発揮する力の解釈から初めてみましょう。

$\displaystyle F = kx$

(16)

でしたね。この式(16)をご覧になればわかるように力[N]は[m]に対して[N/m]で比例しています。例えば力[N]を[N]として一定に保ったときのことを考えてみましょう。そうすると次のことが言えます。

[N/m]が大きくなれば小さな伸び[m]で[N]を発揮する。
[N/m]が小さいと伸び[m]が大きくならないと[N]の力を発揮することは出来ない。

つまり言い換えると同じ力[N]を加えたときの伸びの違いという観点から、[N/m]が小さいバネは軟らかいバネで、大きいバネは硬いバネということになります。

同じ力[N]を加えたときの振る舞いの違いを図29に示します。どちらにも同じ力を加えていることに注意してご覧下さい。

**図 29:** 同じ力を加えたときの軟らかいバネと硬いバネ

バネ1とバネ2を直列につないで力[N]で伸ばしたとき、そのどちらのバネにも同様に[N]の力がかかっていました。そしてそのバネ内の各1巻きのバネにも同じ力[N]がかかっていましたよね。

1巻き1巻きに力[N]を加えられてそれぞれが同じだけもちろんバネ1内とバネ2内の1巻きは別物ですから伸び量は違いますが…伸びることによりバネ1だけ、またはバネ2だけのときよりも、より伸びてしまうわけです。

**図 30:** バネの伸びの比較

したがって、2つのバネを直列接続するとそのどちらにも同様の力が加わることにより、1本だけのときよりも伸びが $+\alpha$ されるために、同じ力しか加えなくても軟らかくなった感じがします。当然、計算によってもバネ定数がより小さくなることを確認できるわけです。

つまりこの軟らかくなるという意味合いを出すのに式(12)の $\frac{1}{K}= \frac{1}{k_1} + \frac{1}{k_2}$ という表し方は好きではないんです。直感的に掴み辛いですから。ですから私のお薦めは式(13)の $K = \frac{k_1k_2}{k_1 + k_2}$ の形です。小さい方よりも小さくなる感じがよく出ていて素敵な式です。

△上へ戻る

直列接続の概念 | バネの直列接続 | 公式の導出 | 式のイメージ | より深く理解する

ホーム＞物理のトップページ＞目次＞力学とは＞力の種類＞バネの直列接続